In our vast, interconnected, and (dare I say infinitely) complex universe, the only certainty is uncertainty.
And yet, intriguingly, while we may never grasp the full picture, our minds come equipped with tools that help us navigate this world, weaving intricate (and hopefully informative) narratives from just snippets of the “grand tableau”.
Bayesian inference is one mathematical formulation/representation of this innate skillset.
Let’s briefly delve into the world of Bayesian inference, from the humble beginnings of a coin toss to its application in modern AI paradigms.

Imagine flipping a coin. Simple, right?
We typically assume that the chances of getting a head or a tail are even. But what if I told you that the coin is biased and the likelihood isn’t 50/50? To what extent would you believe me?
This is where Bayesian inference comes in.
In its essence, Bayesian inference is about updating our beliefs after considering new data.
In the Bayesian statistics framework, we represent our initial belief (prior) about the coin’s bias, see how the coin behaves (observed data), and then revise the belief (posterior) accordingly.
To demonstrate, let’s simulate this in Python:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
# Setting the parameters
true_bias = 0.6 # The true bias of the coin
num_flips = 100 # The number of flips we will observe
# Flipping the coin
np.random.seed(0)
flips = np.random.rand(num_flips) < true_bias
num_heads = np.sum(flips)
# Our belief about the bias of the coin before observing flips
prior = beta(1, 1)
# Our belief after observing the flips
posterior = beta(1 + num_heads, 1 + num_flips - num_heads)
# Plotting the results
x = np.linspace(0, 1, 1002)[1:-1]
plt.plot(x, prior.pdf(x), label='Prior')
plt.plot(x, posterior.pdf(x), label='Posterior')
plt.legend()
plt.show()
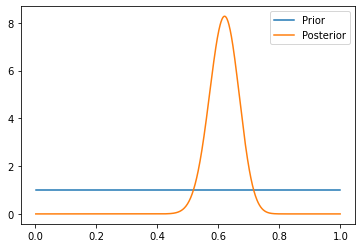
This script first simulates 100 coin flips from a coin with a true bias of 60% towards heads. We then use a beta distribution as our prior belief about the coin’s bias.
A Beta distribution, denoted Beta(α, β), is a family of continuous probability distributions defined on the interval [0, 1] that is commonly used to model the distribution of random variables limited to intervals of finite length. It’s a distribution that’s commonly used in Bayesian statistics because it can take many shapes and it naturally models a probability.
In the code above, we make no assumptions about the prior likelihood of the coin. After observing the flips, we update our belief to form the posterior distribution.
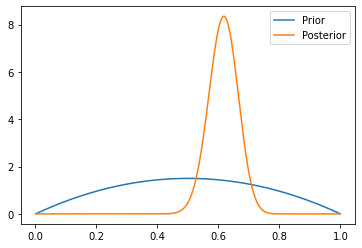
And the result using the same code, but changing “prior = beta(2, 2)” to model our expectation of 50/50 as the prior likelihood (allowing for some variance around this, recognizing that our belief could be incorrect):
The power of Bayesian inference, however, isn’t just limited to understanding biased coins.
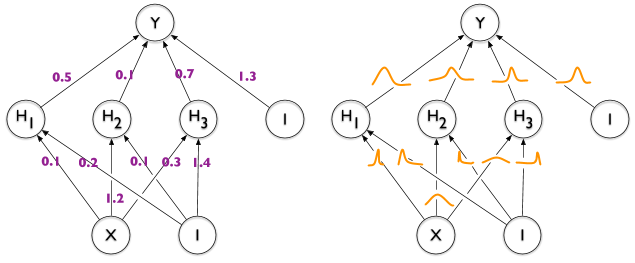
Take neural networks, for instance. Applying the Bayesian framework to neural nets allows for a probabilistic interpretation of the network.
Traditional neural networks provide point estimates, giving the best parameters given the data. Yet, they do not provide a measure of uncertainty with these parameters.
Bayesian neural networks, on the other hand, offer a distribution over possible parameter values, enabling us to understand the model’s certainty and use it for decision making.
The beauty of Bayesian inference is that it provides a robust mathematical tool to navigate through uncertainty, be it in simple systems like coin flipping or complex ones like neural networks.
By continuously updating our beliefs as new data comes in, we create models that not only understand the current situation but are also prepared to incorporate future data efficiently.
Embracing uncertainty through tools like Bayesian inference is not just advantageous, it’s essential. And as we continue to develop new technologies and algorithms in AI and predictive modeling, the principles of Bayesian inference will undoubtedly continue to guide our way.